초보자를 위한 회귀분석 완벽 가이드
🔎 목차 📈
1. 회귀분석이란?
2. 회귀분석의 기본 가정
3. 선형회귀 (Linear Regression)
4. 최소제곱법 (Least Squares Method)
5. 결정계수 (R², Coefficient of Determination)
6. 다중공선성 (Multicollinearity)
7. 특이 행렬 문제
🧩1. 회귀분석이란?
회귀분석(Regression Analysis)은 독립변수(X)와 종속변수(Y) 간의 관계를 통계적 방법으로 모델링하여 데이터를 이해하고 예측하는 분석 기법입니다.
예를 들어, 광고비(독립변수)와 매출(종속변수)의 관계를 분석하여 광고비가 증가하면 매출이 얼마나 증가할지 예측할 수 있습니다.
🔹 독립변수(X): 설명 변수, 입력 변수 (예: 광고비, 공부시간 등)
🔹 종속변수(Y): 반응 변수, 출력 변수 (예: 매출액, 시험 점수 등)
🧩 2. 회귀분석의 기본 가정
회귀분석을 수행하기 위해서는 몇 가지 기본 가정을 만족해야 합니다.
✅ 1️⃣ 선형성 (Linearity)
독립변수(X)와 종속변수(Y) 간의 관계가 직선 형태를 따라야 합니다.
📌 검토 방법: 산점도(Scatter Plot)를 그려서 데이터가 직선 형태를 따르는지 확인합니다.
✅ 2️⃣ 독립성 (Independence)
오차항(Residuals, 예측값과 실제값의 차이)들이 서로 독립적이어야 합니다.
📌 검토 방법: 더빈-왓슨(Durbin-Watson) 검정을 수행하여 독립성을 확인합니다.
✅ 3️⃣ 등분산성 (Homoscedasticity)
잔차(오차)의 분산이 일정해야 합니다. 즉, 데이터의 분포가 특정 구간에서만 집중되지 않고 전체적으로 일정해야 합니다.
📌 검토 방법: 잔차 그래프(Residual Plot)를 확인하여 패턴이 없는지 살펴봅니다.
✅ 4️⃣ 정규성 (Normality)
오차항이 정규분포를 따라야 합니다. 이는 회귀계수의 신뢰성을 높이는 중요한 조건입니다.
📌 검토 방법: 히스토그램과 Q-Q Plot을 활용하여 잔차의 정규성을 평가합니다.
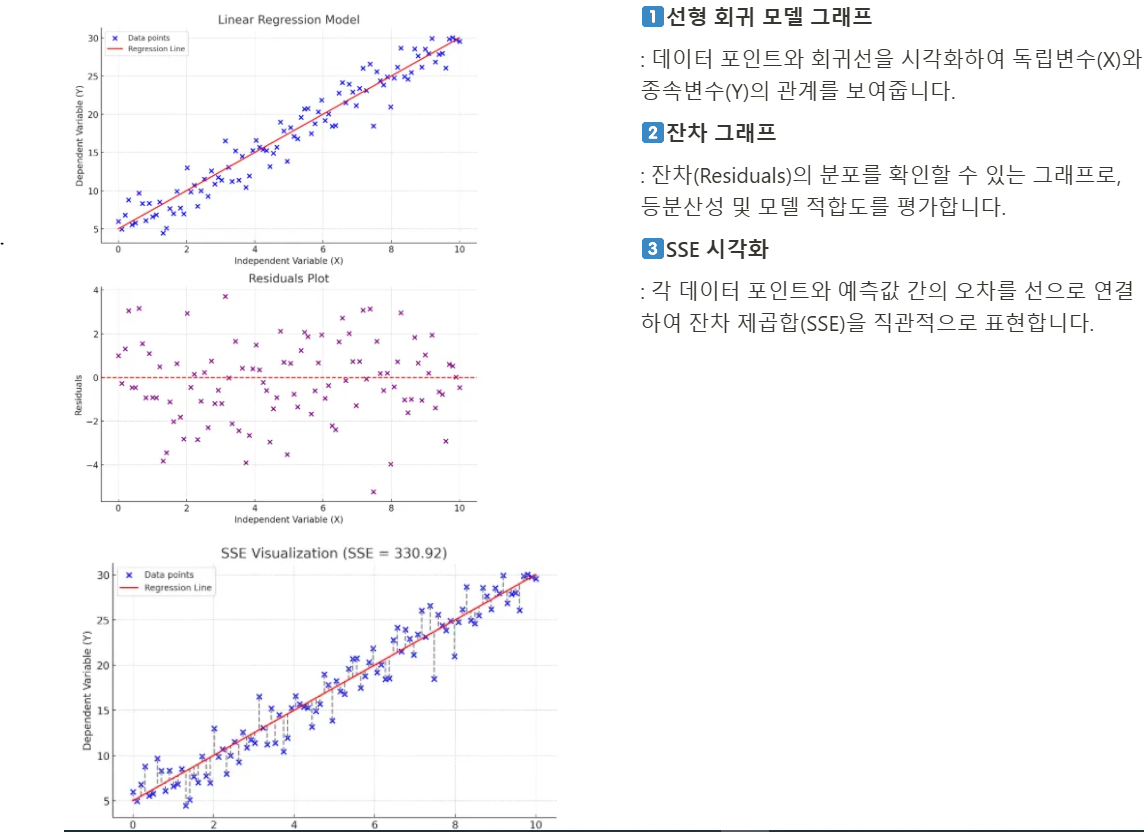
🧩3. 선형회귀 (Linear Regression)
선형회귀는 가장 기본적인 회귀분석 기법으로, 데이터 간 관계를 직선으로 나타냅니다.
🔹 선형회귀식
📌 회귀식: 📊Y = aX + b
- a (기울기): X가 1 증가할 때 Y의 변화량
- b (절편): X가 0일 때 Y의 값
💡 예제:
광고비(X)가 10만 원 증가할 때 매출(Y)이 5만 원 증가한다면, 회귀식은 Y = 5X + b가 됩니다.
🧩4. 최소제곱법 (Least Squares Method)
회귀 분석의 목표는 실제값(Y)과 예측값(Y^) 간의 차이를 최소화하는 것입니다.
✅ 목표: 오차(잔차)를 최소화하여 회귀 계수 추정 ✏️
📌 잔차(Residuals) 계산
📌 잔차 = 실제값(Y) - 예측값(Y^)
잔차의 제곱합(SSE, Sum of Squared Errors)을 최소화하여 최적의 회귀 계수를 찾습니다.

🧩 5. 결정계수 (R², Coefficient of Determination)
회귀 모델이 데이터를 얼마나 잘 설명하는지를 나타내는 지표입니다.
- 모델의 설명력을 평가하는 지표 💡
📌 R² 값의 의미
- R² = 0: 모델이 데이터를 설명하지 못함
- R² = 1: 모델이 데이터를 완벽하게 설명
- 일반적으로 0.7 이상이면 좋은 모델
📌 계산 공식
R² = (설명된 변동) / (전체 변동)
🧩 6. 다중공선성 (Multicollinearity)
다중공선성이란 독립변수들 간의 상관관계가 매우 높은 경우를 의미하며, 이는 모델의 신뢰도를 낮출 수 있습니다.
- 문제: 독립변수들 간 높은 상관관계로 인해 모델 신뢰도 저하 ⚠️
📌 다중공선성 확인 방법
✅ 상관 행렬 확인: 독립변수 간의 상관계수를 분석합니다.
✅ 분산 팽창 요인 VIF(Variance Inflation Factor) 계산:
- VIF > 5: 다중공선성 가능성 존재
- VIF > 10: 심각한 다중공선성
📌 해결 방법
🚀 상관관계가 높은 변수 제거
🚀 주성분 분석(PCA) 활용
🚀 릿지/라쏘 회귀로 정규화
🧩 7. 특이 행렬 문제 (Singular Matrix Problem)
회귀 분석에서 독립변수들이 서로 선형 종속적인 경우, 공분산 행렬이 특이 행렬이 되어 회귀 계수를 구할 수 없게 됩니다.
- 문제: 공분산 행렬이 선형 종속적인 경우 발생 🚨X'X
- 계수 추정 불안정, 예측 정확도 저하, 통계적 유의성 왜곡 가능.
📌 문제 발생 원인
- 독립변수들 간에 완벽한 상관관계가 있는 경우
- 불필요한 변수가 포함된 경우
📌 해결 방법
✅ 독립변수 개수를 줄이거나 상관관계가 높은 변수를 제거
✅ 데이터 변환 (예: 차분, 표준화)
📌 마무리
이 글에서는 회귀분석의 개념부터 기본 가정, 선형회귀, 최소제곱법, 결정계수, 다중공선성, 특이 행렬 문제까지 초보자도 이해하기 쉽게 설명했습니다.
🔎 요약
✅ 회귀분석은 독립변수와 종속변수 간의 관계를 분석하는 기법
✅ 기본 가정(선형성, 독립성, 등분산성, 정규성)을 만족해야 함
✅ 선형회귀의 핵심 개념: 회귀식(Y = aX + b)과 최소제곱법
✅ 모델 성능 평가를 위한 결정계수(R²) 활용
✅ 다중공선성과 특이 행렬 문제 해결 방법
이제 여러분도 회귀분석을 활용하여 데이터를 분석하고 예측하는 능력을 키워보세요! 🚀
🛒 고객 충성도를 측정하는 리텐션 분석을 알고 싶다면 여기를 클릭 ⏳
'IT' 카테고리의 다른 글
| [TIL] 데이터 리터러시_23일차(데이터 리터러시 Part2) (0) | 2024.04.29 |
|---|---|
| [TIL] 데이터 리터러시_22일차(데이터 리터러시 Part1) (0) | 2024.04.26 |
| [TIL] kaggle 와인 데이터 분석_18일차(탐색적 데이터 분석(EDA),논문을 통한 인사이트) (0) | 2024.04.23 |
| [TIL] kaggle 와인 데이터 분석_17일차(프로젝트 진행 순서,전처리,데이터 형식) (0) | 2024.04.23 |
| [TIL/SQL코딩 테스트] Lv.1 문제 해설_16일차(DISTINCT,HAVING,LIMIT,COALESCE ) (0) | 2024.04.16 |



